Examples To Find Rank Of A Matrix

For a 2 4 matrix the rank can t be larger than 2 when the rank equals the smallest dimension it is called full rank a smaller rank is called rank deficient.

Examples to find rank of a matrix.

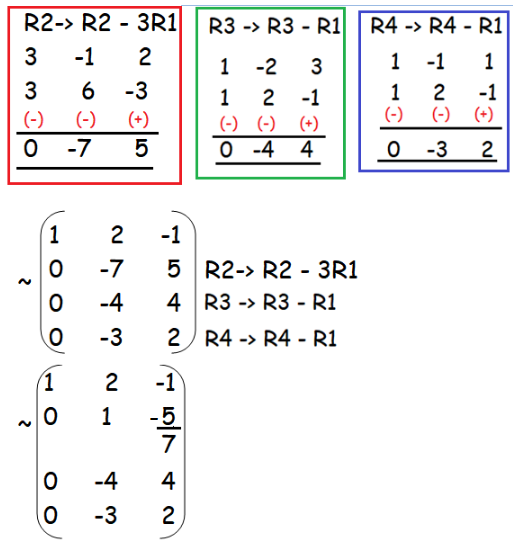
For example the rank of the below matrix would be 1 as the second row is proportional to the first and the third row does not have a non zero element. Find the rank of the matrix. First because the matrix is 4 x 3 its rank can be no greater than 3. Problem 646 a find all 3 times 3 matrices which are in reduced row echelon form and have rank 1.

Perform the following row operations. Rank of a matrix and some special matrices. Consider the third order minor. This method assumes familiarity with echelon matrices and echelon transformations.

Since there are 3 nonzero rows remaining in this echelon form of b example 2. Pick the 1st element in the 1st column and eliminate all elements that are below the current one. In this section we describe a method for finding the rank of any matrix. B find all such matrices with rank 2.

Click here if solved 92 add to solve later. 1 2 3 2 4 6 0 0 0 how to calculate the rank of a matrix. Consider the third order minor 6 0. A rectangular array of m x n numbers in the form of m rows and n columns is called a matrix of order m by n written as m x n matrix.

To calculate a rank of a matrix you need to do the following steps. How to find matrix rank. This corresponds to the maximal number of linearly independent columns of this in turn is identical to the dimension of the vector space spanned by its rows. In this tutorial let us find how to calculate the rank of the matrix.

Gaussian elimination method using this definition we can calculate the rank by employing the gaussian elimination method the gaussian elimination method reduces matrix so that it becomes easier for us to find the rank under these three conditions we exclude a row or a column while calculating the ranks of the matrices using the gaussian elimination method. Find the rank of the matrix. The rank is at least 1 except for a zero matrix a matrix made of all zeros whose rank is 0. Rank is thus a measure of the nondegenerateness of the system of linear equations and linear transformation encoded by.

Therefore at least one of the four rows will become a row of zeros. Let a order of a is 3x3 ρ a 3. In linear algebra the rank of a matrix is the dimension of the vector space generated or spanned by its columns. Find the rank of the matrix.

Let a order of a is 3x3 ρ a 3. There is a minor of order 3 which is not zero ρ a 3.